Unit 3 test study guide parent functions and transformations delves into the fundamental concepts of parent functions and their remarkable transformations, providing a solid foundation for understanding the intricacies of higher-level mathematics.

This guide unravels the nature of parent functions, including linear, quadratic, exponential, and logarithmic functions, highlighting their distinctive characteristics and properties. It then explores the concept of transformations, such as translations, reflections, and stretches, and their profound impact on the graphs and equations of parent functions.

Unit 3 Test Study Guide: Parent Functions and Transformations

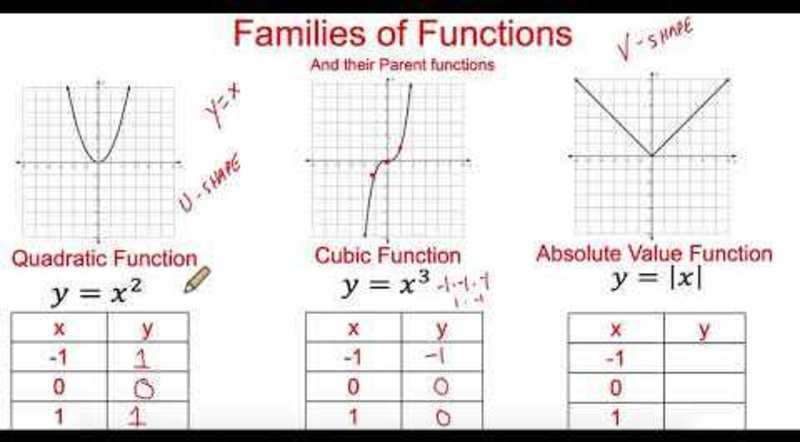
This study guide provides a comprehensive overview of the key concepts and skills related to parent functions and transformations, which are essential topics in algebra and higher mathematics. Understanding these concepts is crucial for success in Unit 3 and beyond.

Parent Functions

Parent functions are basic functions that serve as building blocks for more complex functions. They have distinct characteristics and properties that define their behavior and shape.

• Linear function:f(x) = mx + b, where m is the slope and b is the y-intercept. It represents a straight line.
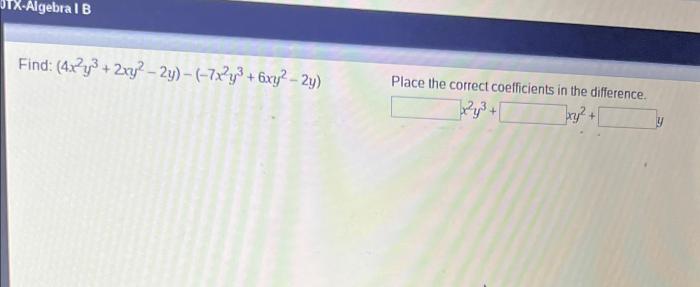
• Quadratic function:f(x) = ax² + bx + c, where a, b, and c are constants. It represents a parabola.
• Exponential function:f(x) = aˣ, where a is a positive constant. It represents a curve that increases or decreases rapidly.
• Logarithmic function:f(x) = log _a(x), where a is a positive constant. It represents the inverse of an exponential function.

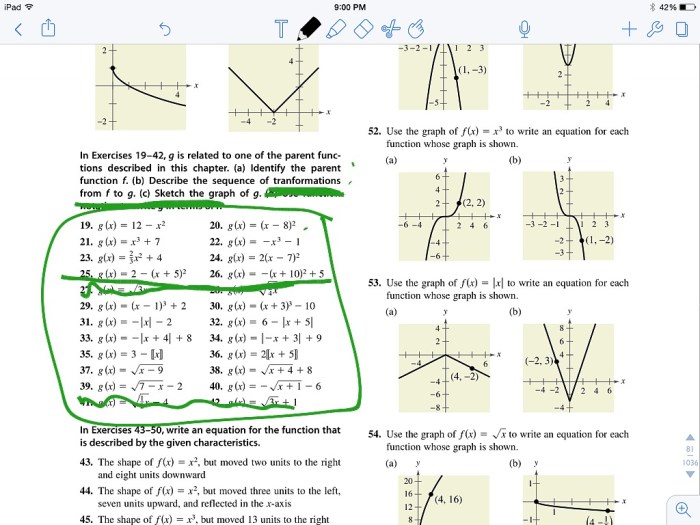
Transformations of Parent Functions

Transformations are operations that can be applied to parent functions to create new functions with different graphs and equations. They allow us to manipulate the shape, position, and orientation of a function.

• Translations:Moving the function horizontally (x-axis) or vertically (y-axis) by adding or subtracting constants.
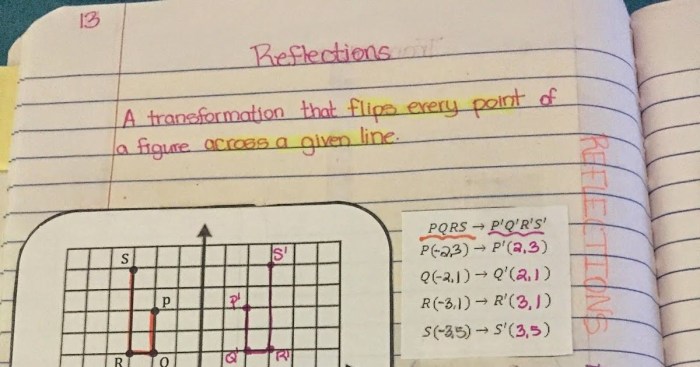
• Reflections:Flipping the function across the x-axis or y-axis by multiplying the equation by -1.
• Stretches:Changing the slope or amplitude of the function by multiplying the equation by a constant.

Applications of Transformations, Unit 3 test study guide parent functions and transformations

Transformations have practical applications in various fields:

• Physics:Modeling projectile motion, harmonic motion, and other physical phenomena.
• Engineering:Designing bridges, buildings, and other structures.
• Economics:Analyzing market trends, forecasting demand, and optimizing production.
• Data analysis:Adjusting data sets to remove bias or highlight patterns.

Q&A: Unit 3 Test Study Guide Parent Functions And Transformations

What is the significance of parent functions?

Parent functions serve as building blocks for more complex functions, allowing us to understand the fundamental behaviors and properties of various mathematical relationships.

How do transformations affect the graph of a function?

Transformations shift, flip, or stretch the graph of a parent function, altering its domain, range, and key features.

What are the practical applications of transformations?

Transformations find widespread use in fields like physics, engineering, and economics, enabling us to model real-world phenomena and solve complex problems.