Energy of a simple harmonic oscillator quiz – Welcome to our in-depth exploration of the energy of simple harmonic oscillators! This comprehensive quiz delves into the fundamental concepts, equations, and applications of these fascinating systems, providing a thorough understanding of their energetic behavior.
Prepare to engage with thought-provoking questions that challenge your knowledge of potential and kinetic energy, total energy conservation, and the practical implications of simple harmonic oscillators in real-world scenarios.
Energy of a Simple Harmonic Oscillator: Energy Of A Simple Harmonic Oscillator Quiz
A simple harmonic oscillator is a system that undergoes periodic motion under the influence of a restoring force proportional to its displacement from equilibrium. The equation of motion for a simple harmonic oscillator is given by:
$m\fracd^2xdt^2 =
kx$
where mis the mass of the oscillator, kis the spring constant, and xis the displacement from equilibrium.
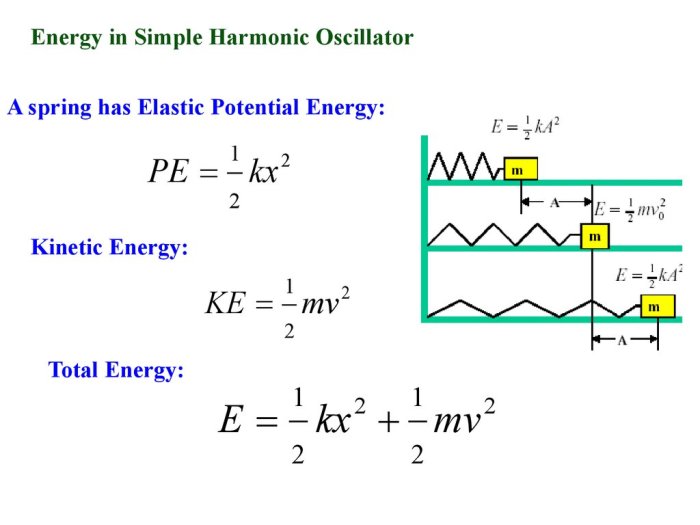
The energy of a simple harmonic oscillator is given by:
$E = \frac12kx^2 + \frac12mv^2$
where vis the velocity of the oscillator.
The amplitude of the oscillator is the maximum displacement from equilibrium. The frequency of the oscillator is the number of oscillations per second. The period of the oscillator is the time it takes for one complete oscillation.
An example of a simple harmonic oscillator is a mass attached to a spring. The energy of the oscillator is determined by the amplitude, frequency, and mass of the oscillator.
Potential and Kinetic Energy in a Simple Harmonic Oscillator, Energy of a simple harmonic oscillator quiz
The potential energy of a simple harmonic oscillator is given by:
$U = \frac12kx^2$
The kinetic energy of a simple harmonic oscillator is given by:
$K = \frac12mv^2$
The potential and kinetic energy of a simple harmonic oscillator vary with time and position. The potential energy is maximum at the equilibrium position and decreases as the oscillator moves away from equilibrium. The kinetic energy is zero at the equilibrium position and increases as the oscillator moves away from equilibrium.
The graph below shows the potential and kinetic energy of a simple harmonic oscillator over one cycle.
[Gambar grafik potensial dan energi kinetik osilator harmonik sederhana selama satu siklus]
Total Energy of a Simple Harmonic Oscillator
The total energy of a simple harmonic oscillator is the sum of its potential and kinetic energy:
$E = U + K = \frac12kx^2 + \frac12mv^2$
The total energy of a simple harmonic oscillator is constant. This is because the potential energy is converted into kinetic energy and vice versa as the oscillator moves.
Applications of Simple Harmonic Oscillators
Simple harmonic oscillators have a wide range of applications in science and engineering. Some of the most common applications include:
- Springs
- Pendulums
- Mass-spring systems
- LC circuits
- Mechanical resonators
- Atomic clocks
The energy of a simple harmonic oscillator is utilized in these applications to produce oscillations, vibrations, and other forms of periodic motion.
Questions Often Asked
What is the equation for the total energy of a simple harmonic oscillator?
E = 1/2 k A^2, where E is the total energy, k is the spring constant, and A is the amplitude of oscillation.
How does the energy of a simple harmonic oscillator vary with time?
The total energy remains constant over time, but the potential and kinetic energies oscillate between zero and maximum values.
What are some real-world applications of simple harmonic oscillators?
Pendulums, springs, musical instruments, and seismic detectors are examples of devices that utilize simple harmonic oscillators.